Chapter 1: Understanding the Nature of Pi

In 2019, my exploration into the concept of Sy? led me to propose that our comprehension of Pi remains incomplete. I contended that our perception of both Pi and circles has been fundamentally flawed. While the conventional understanding of Pi serves us well, it ultimately remains an approximation. This means that every measurement derived from it is similarly approximate, introducing minuscule errors that can escalate significantly in larger applications.

Everything you're about to discover is not merely an approximation; it is precise and can be verified through replication and cross-examination. As the saying goes, extraordinary claims necessitate extraordinary evidence.

Surprisingly, Pi is quite straightforward and not exclusively tied to circles. Its connection to circles becomes clearer as we delve into the details of this informal yet comprehensive "proof."

Let's embark on a simple construction by examining four geometric shapes: a square, a circle, a triangle, and a hexagon. While it's common to inscribe these shapes within a square or circle, a frequent error arises here. I have personally encountered this mistake in my constructions. Triangles, hexagons, and other polygons do not necessarily touch at what seem to be their vertices or edges. Although we can manipulate them to appear perfectly aligned, this introduces approximations and subtle errors.

These approximations can lead to significant misunderstandings regarding the constants themselves. What defines the golden ratio as "golden"? Why does Pi appear in so many contexts? Let’s set the stage for our construction and outline some variables.

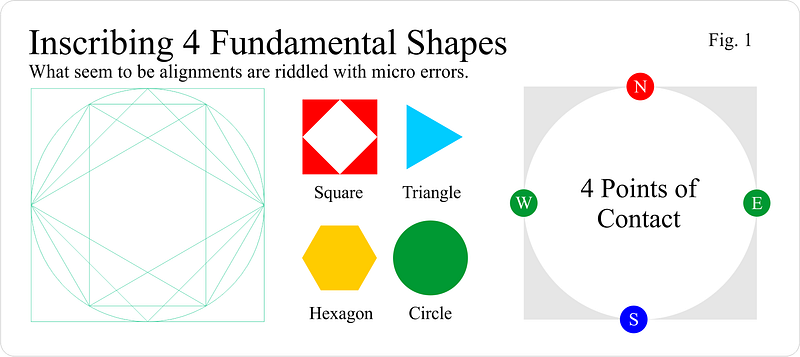
The illustration above breaks down the essential logic of a circle. This logic is critical and precise. Circles and shapes are determined by the points and quadrants within a defined space. While the values can vary, there remains an underlying pattern and structure that exists at any scale.

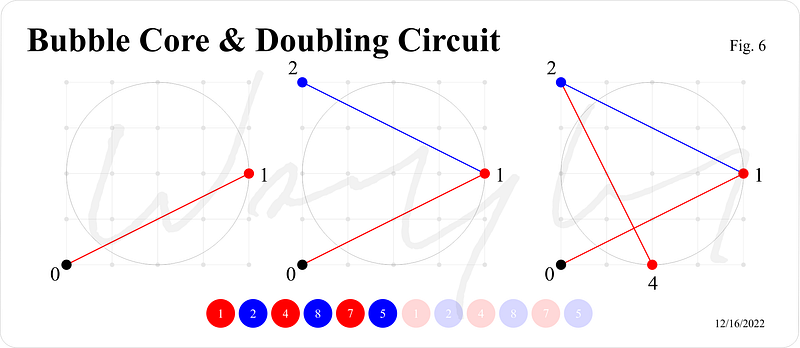
I propose that focusing solely on the radius and center of a circle is an incomplete perspective. The Bubble Core serves as a fundamental geometrical and mathematical framework. Unlike approximations, it is exact and universally applicable across all circles and shapes, regardless of size or dimension.

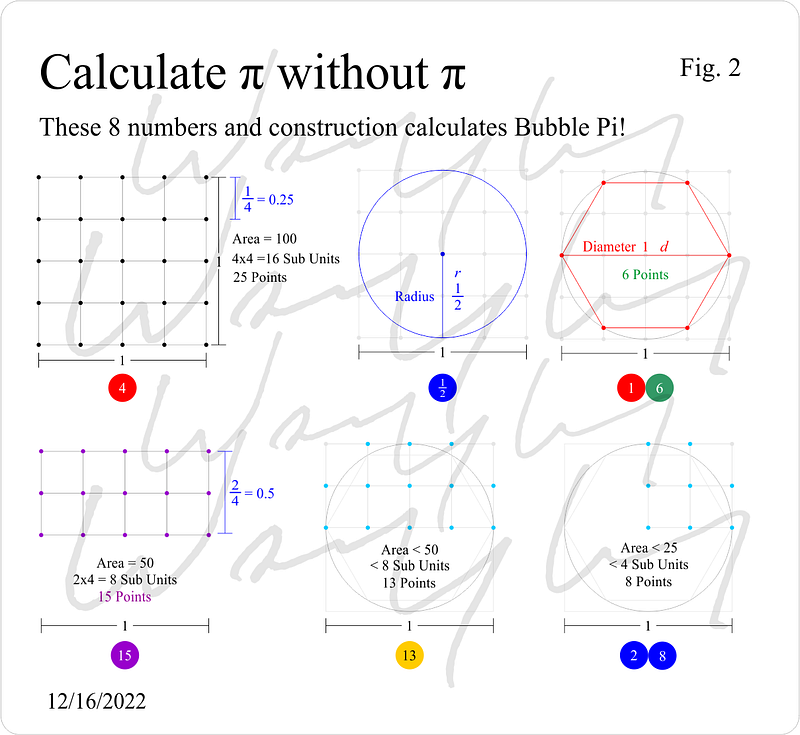
Many scholars before me have recognized the significance of the inverse square law and the various mathematical constants that govern light, gravity, electromagnetic waves, and quantum phenomena. These constants permeate the entire universe.

The interconnectedness of the inverse square law, the doubling circuit, the Bubble Core, and Pi is profound. This recurring digital root pattern within the doubling circuit has been a subject of my earlier research and intriguingly relates to the Synergy constant of 162, which I previously struggled to explain.

When we analyze the eight significant numbers derived from the aforementioned construction, in conjunction with this doubling circuit, we adhere to the same logical framework that we are proposing. Astonishingly, we can compute Pi to a remarkable degree of accuracy without employing radians or Pi itself—something that was once thought impossible!

In discussions of accuracy, we often assess how closely Bubble Pi aligns with the conventional value of Pi. It's crucial to recognize that SyPi and EyPi, though distinct, all relate back to Pi and are consistent with each other. We label Pi as an approximation, suggesting that accuracy is subjective based on context. This is why we encounter varying values of Pi during actual measurements.

We are embarking on a journey to uncover fresh insights into what Pi truly represents and the mechanisms that drive it. The Bubble Core, Bubble Pi, and the Doubling Sequence are pivotal in unlocking this understanding once and for all.

By adhering to the angles and rules of the Bubble Core, combined with the doubling circuit, we unveil some striking truths.

We discover that there are only two feasible paths regardless of the initial orientation. Each path covers the same distance in an identical number of steps, which is clear and evident. However, the angular distance traveled differs significantly.

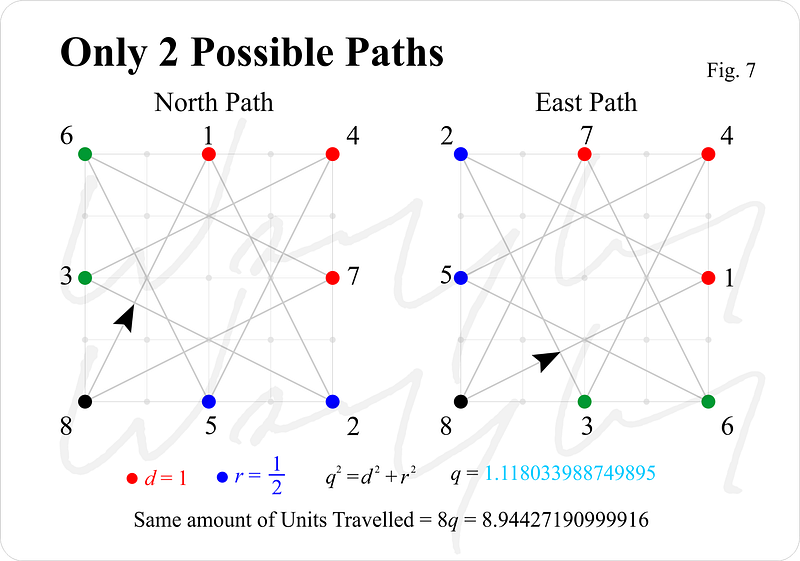
This is where the discussion becomes particularly intriguing. A fundamental question in physics revolves around the speed of light: why is it precisely 299,792,458 meters per second? What accounts for the specific values of other constants?

As I have previously indicated, bubbles and light share a commonality—they both tend to follow the most efficient path. This path may not always represent the shortest distance, but it is the shortest in terms of time. Bubbles connect at angles of 120 degrees, which closely parallels how light reflects and refracts.

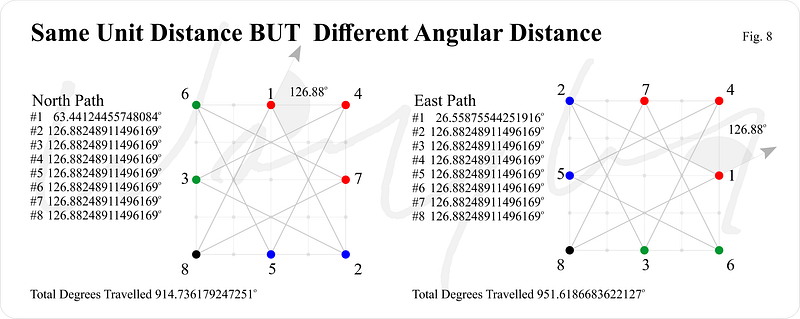
The angle corresponding to the speed of light aligns closely with 120 degrees. This sheds light on the ongoing scientific mystery surrounding why the speed of light is not precisely 300 million meters per second. What have we overlooked?

This enigma has puzzled many until now! I was astounded when I made a recent discovery that clarified everything. The simplicity and intuitiveness of the entire construction became apparent. Everything aligns perfectly without approximations.

Here, for the first time, you will witness how the speed of light can be calculated with remarkable accuracy and logic.

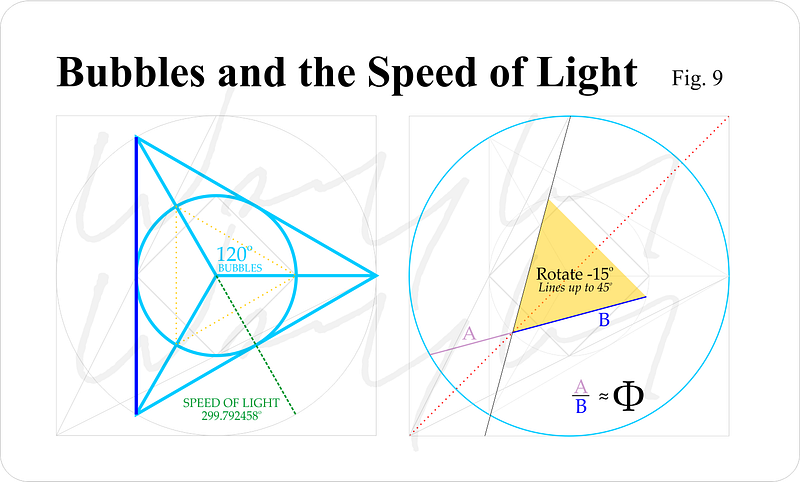
The Synergy constant, the Bubble Core, and the Doubling Sequence illuminate the nature of light and, by extension, our universe in a mechanical sense. They reveal the underlying logic governing all constants—it's truly extraordinary.

Moreover, this precise model suggests that there are two distinct speeds of light: one that we observe and another that remains unidentified or unmeasured. Interestingly, the latter is still slightly below 300 million meters per second but exceeds the "observable" speed of light.

This distinction is significant, as measurements often reveal a duality in results due to the quest for the shortest possible path. Our examination of this model and the doubling circuit indicates that this path is defined by the model, elucidating the presence of irrational numbers, imaginary numbers, and the concept of infinity. We trace the origins of an infinite and repeating cycle within a designated unit of space.

With all these findings being so methodical, logical, and precise, we can make some compelling statements of fact. At its essence, this is all quite simple, akin to Pythagoras' theorem. While complexities may arise from combined elements, the foundational principles remain straightforward.

Additionally, this discovery offers a partial definition of time. If light indeed seeks the quickest temporal path, then the angular movement that determines the speed of light must also represent time.

This intriguing correlation warrants contemplation, especially given the precision and simplicity of the findings.

There are many more revelations to share, but for now, I will leave you to reflect on the implications of this knowledge. In my next post, I will finally delve into the Synergy constant in detail, demonstrating how all of this intricately connects to the Great Pyramid of Giza.

Indeed, they were aware of all this! Not only did they possess this understanding, but there are remarkable facts that substantiate it. Stay tuned, and happy Winter Solstice!

Chapter 2: Video Insights

In this engaging video, titled "Unmasking the Mystery: My Face Reveal Finally Revealed! #facereveal #gtarp #nopixel," the creator shares their long-awaited face reveal, offering insights into their journey and discoveries.

The second video, "One Of The Biggest Mysteries In The Bible Was Finally Revealed," explores deep theological questions and unveils significant revelations, connecting ancient texts to contemporary understanding.