Understanding the Equation: Why 1 + 2 + 3 ... = -1/12 in Physics
Written on
The Paradox of Infinite Sums
The equation 1 + 2 + 3 ... = -1/12 is often met with skepticism due to its perplexing nature. How can an infinite sum of positive integers yield a negative result? Let's explore the underlying reasons behind this surprising conclusion.
Despite appearing nonsensical, the equation has significant applications in physics. Understanding its relevance requires a closer look at the concept of vacuum energy.
Vacuum Energy in Physics
When does this peculiar sum emerge in the realm of physics? It primarily arises in the calculation of vacuum energy, particularly within string theory. In quantum physics, energy is derived from the vibrations of various fields, such as electromagnetic fields. The vacuum energy correlates with the frequencies of these modes, leading to equations like this:
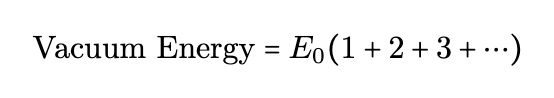
However, physics is grounded in measurable quantities. Since we cannot quantify infinity, the computed vacuum energy cannot logically be infinite either, creating a paradox. Thus, we must reconcile this contradiction.
A Leap of Faith
To progress, we must entertain the possibility that our equation is incomplete. This could indicate that our models are not fully developed. While they may provide results, those results might only be applicable within a specific context.
This situation is akin to a calculator that functions well with small numbers but produces erroneous outputs when faced with very large values. To make sense of the infinite sum, we must account for our lack of understanding—a process termed regularization.
Regularization: Taming the Infinite
To address the discrepancies in the formula, we need to parameterize our inaccuracies. This parameterization must possess certain characteristics:
- It should treat each term uniformly, honoring the symmetries present in the physical world.
- It must taper off for large values of n to appropriately manage the infinite aspects.
- It needs to be adjustable, allowing us to observe varying effects.
In mathematical terms, we introduce a regularizer ( R(n, N) ) that encapsulates our uncertainties in physics. This regularizer should range between 0 and 1, diminishing as n increases. Additionally, N governs the extent of our ignorance. Thus, we can reformulate our sum as follows:
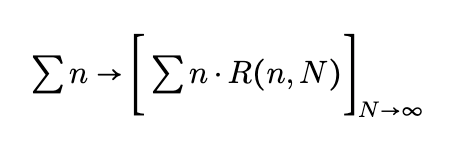
To clarify this concept, let's examine an explicit example of exponential regularization.
Exponential Regularization Explained
The regulator ( e^{-n/N} ) is effective because, with a large N, it minimally affects the terms until we reach substantial n values. The beauty of this regularization lies in its ability to yield exact computations!
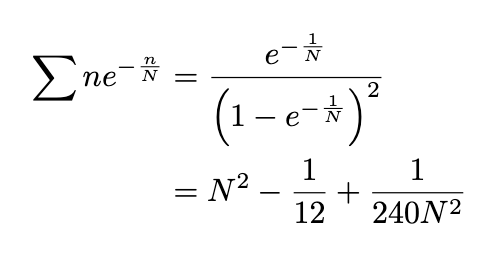
As we let N approach infinity, and by ignoring the infinite ( N^2 ) terms, we discover that ( 1 + 2 + 3 ... = -1/12 ) holds true, albeit under specific conditions.
Addressing Concerns of Ambiguity
This leads to a critical question: how can we disregard infinity without it seeming like a fallacy? The answer lies in the fact that the outcome must be finite, as it represents an observable quantity. The appearance of infinity suggests our theories are incomplete or that our mathematical techniques require refinement. By integrating corrections into our theoretical framework, we can align our models with natural phenomena.
Mathematical Uniqueness
From a mathematical perspective, we can ensure the uniqueness of our answer, provided we adhere to the requirements established by physics-driven regularization. Prof. Terry Tao's blog offers a rigorous proof supporting this assertion.
While theoretical justifications may appear tenuous, experimental validation is the ultimate arbiter. It is feasible to measure the attractive forces resulting from the vacuum energy calculations, as demonstrated in this experimental paper — the results affirm the validity of our approach (albeit in a different but analogous context).
Conclusion: Embracing the Infinite
In conclusion, to comprehend the infinite, we must acknowledge our limitations and amend our results. Fortunately, a consistent and rational method exists to rectify our misunderstandings and yield finite outcomes. Perhaps nature imparts a valuable lesson: humility and groundedness can transform the seemingly impossible into the comprehensible.
Appendix: Riemann Zeta Function Insights
Some articles may hastily link the infinite sum to the Riemann zeta function ( zeta(s) ), defined as follows:
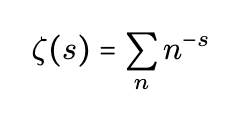
While this substitution yields the correct result, it can lead to confusion, as the definition is valid only for ( s > 1 ). A more robust analysis would necessitate complex analysis techniques. For instance, employing the Abel formula allows us to convert the summation into an integral, where regularization acts as a cap. This intricate manipulation yields results comparable to those obtained through exponential regularization, linking finite terms to ( zeta(2) ), which is intertwined with ( zeta(-1) ) via the zeta reflection identity.
In the first video, "Numberphile v. Math: the truth about 1+2+3+...=-1/12," the complexities of this equation are explored in detail, shedding light on its mathematical implications.
The second video, "ASTOUNDING: 1 + 2 + 3 + 4 + 5 + -", further delves into the astounding nature of this equation, revealing its intriguing aspects and significance.