Understanding the Divisibility Rule for 7: A Comprehensive Guide
Written on
Chapter 1: Introduction to the Divisibility Rule
The divisibility rule for 7 indicates that a number ( N ) is divisible by 7 if you take its last digit, double it, and subtract this from the remaining truncated number after removing the last digit. If the resulting number, which we can denote as ( N' ), is divisible by 7, then ( N ) is also divisible by 7. This process can be repeated, truncating further if needed.
For instance, consider ( N = 826 ):
- Remove the last digit: ( 82 )
- Double the last digit: ( 2 times 2 = 4 )
- Subtract: ( 82 - 4 = 78 )
Since ( 78 ) is divisible by 7, it follows that ( 826 ) is also divisible by 7.
Example I: Take ( N = 826 ):
- ( N' = 82 - (2 times 6) = 82 - 12 = 70 )
- Clearly, 7 divides ( N' = 70 ) and thus ( 7 ) divides ( 826 ).
Example II: Now, let’s analyze ( N = 1234 ):
- ( N' = 123 - (2 times 4) = 123 - 8 = 115 )
- Continuing, ( N'' = 11 - (2 times 5) = 11 - 10 = 1 )
- Since ( 7 ) does not divide ( N'' = 1 ), it implies ( 7 ) does not divide ( 115 ), and hence ( 7 ) does not divide ( 1234 ).
Why does this rule hold true? Let's break it down.
Proof of the Rule
Any number ( N ) can be expressed in a format where each ( a ) corresponds to a digit of ( N ):
For example, for ( 826 ):
[
826 = 8 times 10^2 + 2 times 10^1 + 6
]
Now, let’s analyze ( N' ):
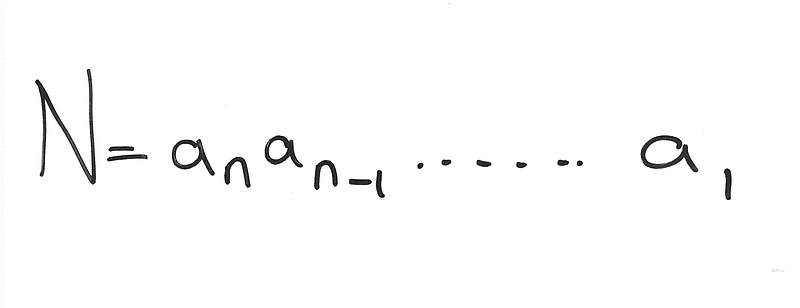
Assuming ( 7 ) divides ( N' ), we aim to prove that ( 7 ) also divides ( N ). By multiplying through by 10, we derive:
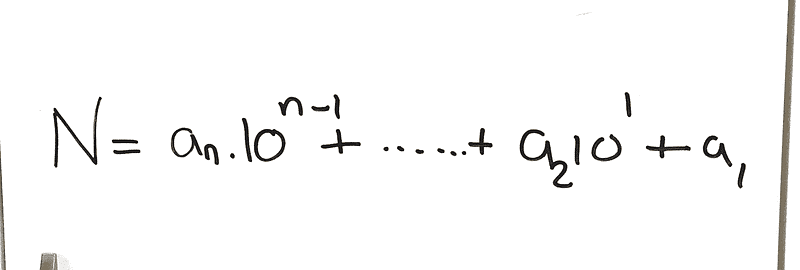
Rearranging gives us:
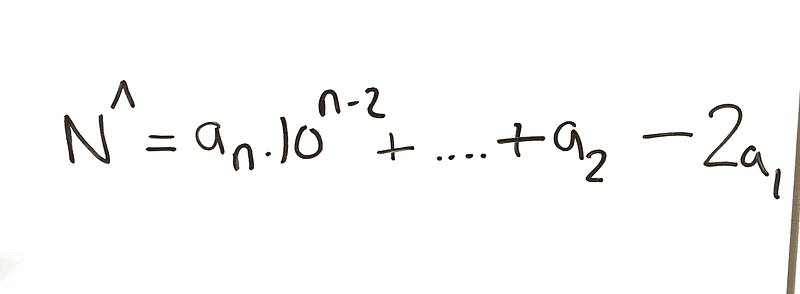
Since ( 7 ) divides ( 21a ) and ( 7 ) divides ( N' ), it follows that ( 7 ) must also divide ( N ).
And that concludes the proof!
Closing Thoughts
Utilize this representation of ( N ) to explore other divisibility rules. For example, ( 3 ) divides ( N ) if the sum of its digits is divisible by ( 3 ). An example is ( 1236 ) because ( 1 + 2 + 3 + 6 = 12 ), which is divisible by ( 3 ). Similarly, ( 11 ) divides ( N ) if the alternating sum of its digits is divisible by ( 11 ). For instance, ( 10901 ) is divisible by ( 11 ) since ( 1 - 0 + 9 - 0 + 1 = 11 ), which is divisible by ( 11 ).
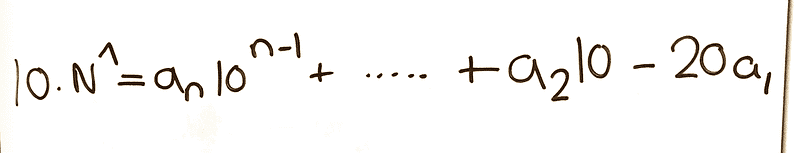
In this video titled "GMAT - Why do divisibility rules work?" you will discover the rationale behind the divisibility rules, including practical examples and a deeper understanding of the topic.
The video "Divisibility Rule for Seven (TANTON Mathematics)" delves into the specifics of the divisibility rule for 7, offering explanations and further examples to enhance comprehension.