# The Ubiquity of the Laplacian: An Intuitive Insight
Written on
Chapter 1: Introduction to the Laplacian
Have you ever pondered why the Laplacian appears so frequently in fields like physics and engineering? Numerous explanations exist, often linked to concepts of symmetry. However, one compelling perspective focuses on the inherent meaning of the Laplacian itself.
Section 1.1: Understanding the Heat Equation
Consider the heat equation:
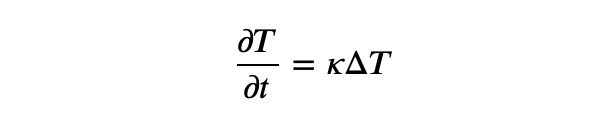
The left side of the equation indicates the rate at which temperature is changing at a particular point, denoted as ?? What factors might influence this change? Intuitively, it seems logical to assume that the temperature at that point would be affected by the temperatures in its surrounding area. If the neighboring region is generally warmer than point ??, we would anticipate an increase in temperature at ??; conversely, if it is cooler, we expect a decrease. This is precisely the information conveyed by the Laplacian!
Section 1.2: The One-Dimensional Case
In one dimension, the Laplacian is defined as follows:
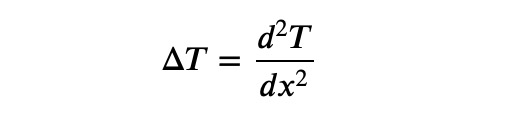
As you might be aware from calculus or similar resources, the second derivative can be represented as a limit:
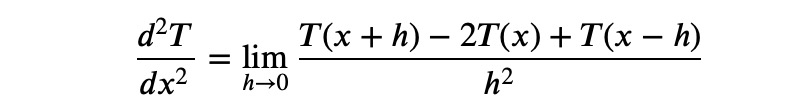
By examining the expression under the limit, we can see that it is proportional to:
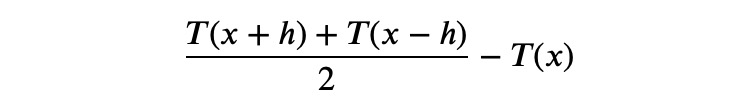
This suggests that the second derivative (or Laplacian) reflects the difference between the function's value at the focal point, ?(?), and the average values of its immediate neighborhood. This logic extends seamlessly into multiple dimensions, providing a clear conceptual foundation for the Laplacian's significance and its frequent appearance in various physical equations, such as the heat equation.
Chapter 2: Broader Implications of the Laplacian
The remarkable aspect of the Laplacian is how a concept rooted in basic calculus can have such extensive implications in physics and engineering. Notably, the Laplacian also features prominently in other fundamental equations, including the wave equation and Schrödinger's equation in quantum mechanics. In these contexts, the Laplacian serves as a metric for how systems evolve or change over time in relation to their surroundings.