Runge-Kutta Methods for Solving ODEs with Python
Written on
Introduction to Numerical Solutions of ODEs
This article illustrates the process of numerically solving ordinary differential equations (ODEs) through the Runge-Kutta (RK) method using Python. ODEs are pivotal in modeling various physical phenomena, such as atmospheric conditions or temperature changes described by Newton’s law of cooling. Additionally, they play a crucial role in analyzing motion over time, where some equations cannot be solved analytically. Mastery in solving ODEs is essential across multiple fields of engineering and science.

Theory Behind Runge-Kutta Methods
The RK methods leverage core principles of numerical differentiation, integration, and Taylor series. For a foundational understanding, it may be beneficial to review related articles listed below.
How Numerical Differentiation Works in Python
A comprehensive guide on numerical differentiation techniques in Python.
How to Perform Numerical Integration in Python
An article detailing methods for evaluating integrals numerically using Python.
Approximating Functions with Taylor Polynomials in Python
A tutorial focused on function approximation through Taylor polynomials.
The goal is to estimate an unknown function ( y ) at a future time ( t ) based on initial conditions and the differential equation governing the evolution of ( y ).
Overview of Ordinary Differential Equations
ODEs describe dynamic systems. A typical first-order ODE, which varies with both space (y) and time (t), is illustrated in Equation 1.
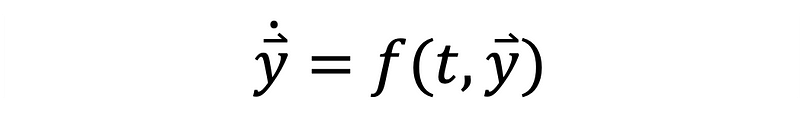
An ODE consists of derivatives with respect to a single variable, and its order is determined by the highest derivative present. An initial value problem (IVP) involves knowing the state of the system at a specific initial time ( t_0 ). With the initial conditions and the ODE, one can project the system's evolution over time through discrete steps.
Example of a Differential Equation
Equation 2 exemplifies a second-order ODE that will be approached numerically.
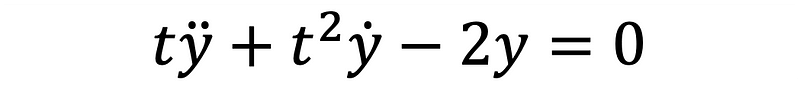
Being a second-order equation, it requires conversion into a system of first-order ODEs. By introducing auxiliary variables defined in Equations 3 and 4, we can facilitate this transformation.
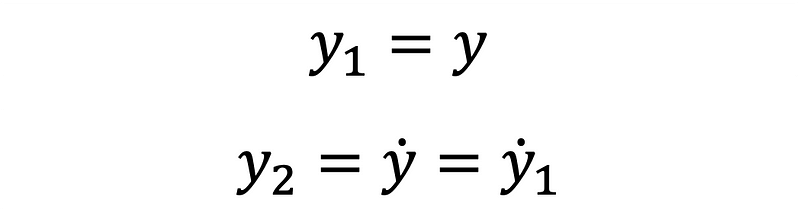
Substituting the variables into Equation 2 allows us to rewrite it as a system of first-order equations as shown in Equations 5 and 6.
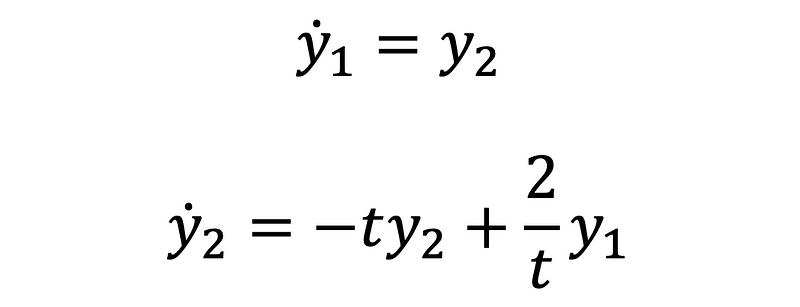
This transformation results in two first-order ODEs, with initial conditions given as ( y_0 = 0 ) and ( y'_0 = 1 ) at ( t_0 = 1 ) second. These conditions are flexible, allowing users to experiment with different values to observe their impact on the system state. In practical applications, such as modeling a mass-spring-damper system, these conditions represent physical concepts like starting position and velocity.
The following video provides an in-depth look at coding a fourth-order Runge-Kutta integrator in both Python and Matlab, which will enhance your understanding of the methods discussed.
Runge-Kutta Method Explained
The main objective remains to evaluate ( y ) at a future time ( t ), for instance, at ( t = 4 ) seconds, utilizing the initial state and the differential equation that governs ( y )'s change over time. Thus, Equation 7 represents a general formula for the single-step Runge-Kutta method.
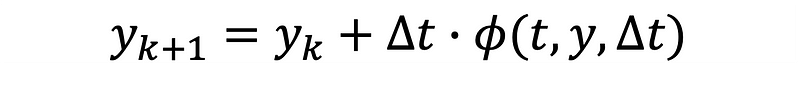
The function ( f(t, y, Delta t) ) serves as an average of the slope of ( y ) over the time interval ( t_0 ) to ( t_n ), as depicted in Figure 1.
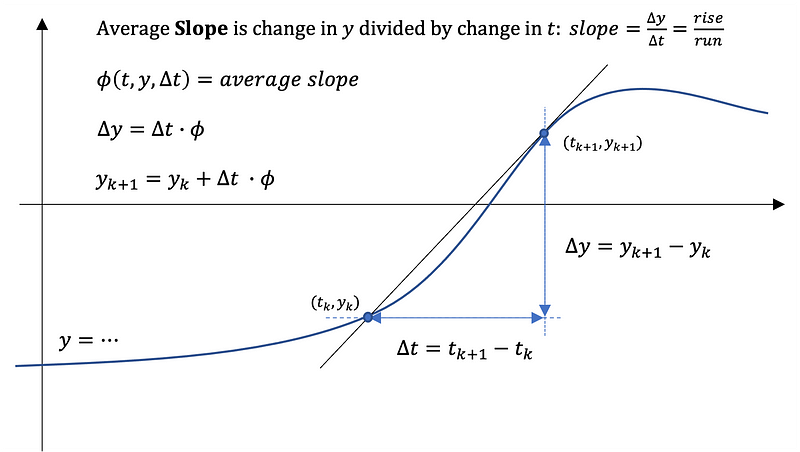
The RK methods offer a robust technique for computing the average slope of the vector field in the vicinity of the current point ( (t_0, y_0) ), leading to improved accuracy in approximating ( y ).
Equations 8 to 11 illustrate the derivatives at various points along the interval ( (t_0, t_n) ).
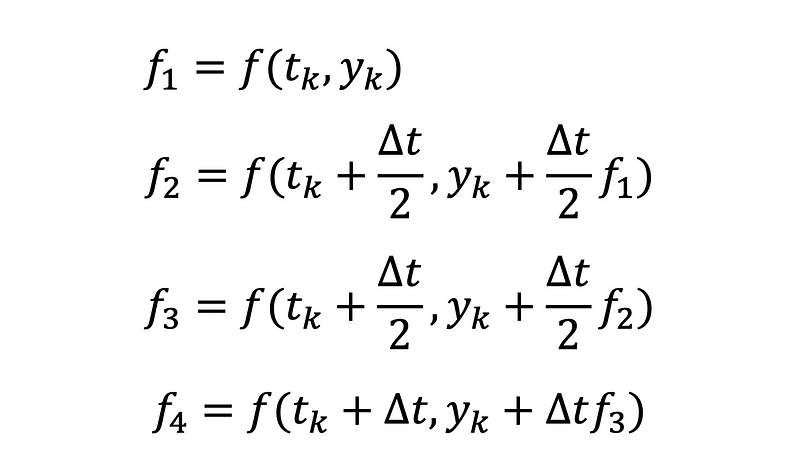
By applying multiple estimations and calculating a weighted average, the precision of the final approximation of ( y_n ) is enhanced. Equation 12 below shows the single-step fourth-order RK4 weighted sum for approximating the next state.
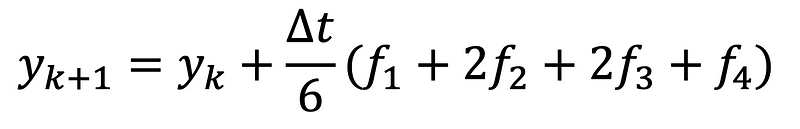
With four evaluations of the vector field and specified weights, the error remains of order ( O(Delta t^4) ). Thus, the RK method's accuracy is comparable to that of Taylor series expansions.
The following video explains how to solve a system of first-order ODEs using the RK4 method in Python, providing practical insights into the coding process.
Results of the Integration
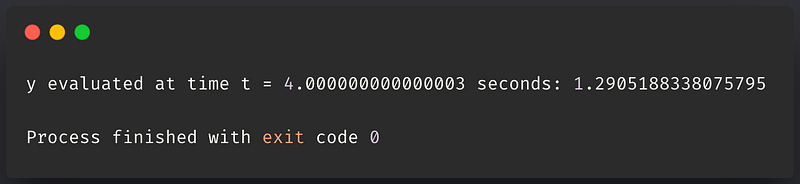
Figure 2 presents the output from the console after executing the code to estimate ( y ) at 4 seconds, yielding an approximate value of 1.29. Throughout each iteration, the variable state_history captures the system’s state.
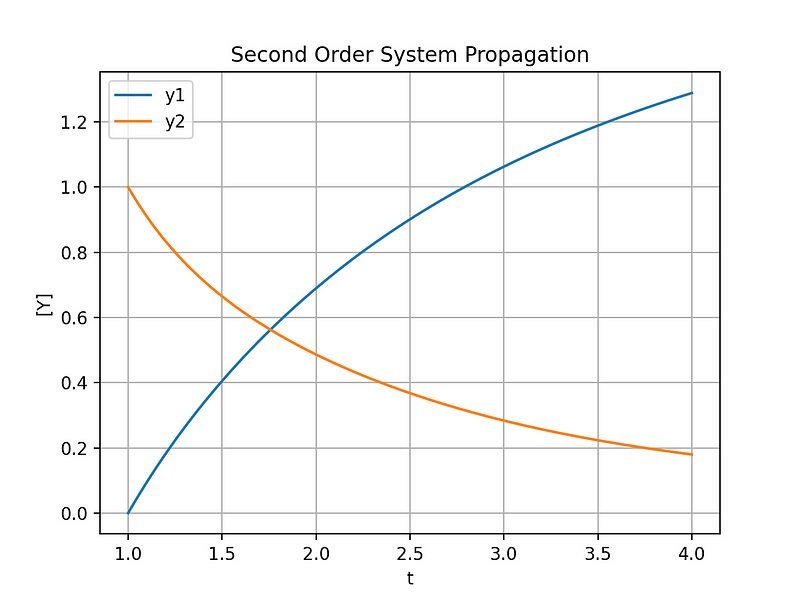
The state_history variable is crucial for analysis and visualization purposes. Figure 3 displays the history of the state variables ( [y_0, y_1] ) from ( t_0 = 1 ) to ( t = 4 ) seconds.
Conclusion
In MATLAB, the methods ode23 and ode45 correspond to the RK2 and RK4 methods, respectively. This article has outlined a Python implementation for the RK4 method, a numerical integration technique for solving first-order ordinary differential equations. Although methods like Euler's method are also widely used for ODE solutions, RK4 provides superior accuracy at the expense of increased computational resources.
Explore the linked article for applying the RK4 method to an orbital mechanics problem using Python.
The Two-Body Problem in Python
Visualizing the motion of two bodies due solely to their mutual gravitational attraction
levelup.gitconnected.com
See Gist 4 for the complete Python code.
References
[1] ME564 Lecture 18: Runge-Kutta Integration of ODEs and the Lorenz Equation
[2] Orbital Mechanics for Engineering Students — Numerical Integration Section 1.8
[3] The Runge-Kutta Family of Integrators