Matrix Addition

Adding matrices is a simple operation, but it requires that both matrices share the same dimensions. Here's an example:

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

b = np.array([[3, 2, 1], [6, 5, 6], [1, 1, 1]])

print('A=', a)

print('n')

print('B=', b)

print('n')

print('Shape of A is:', a.shape)

print('Shape of B is:', b.shape)

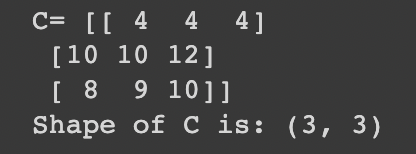
In this case, both matrix A and matrix B are 3x3, allowing us to perform addition by summing corresponding elements:

c = a + b

print('C=', c)

print('Shape of C is:', c.shape)

Matrix Subtraction

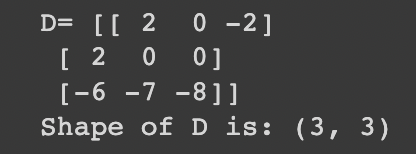
Subtraction in matrices follows the same principle as addition. Essentially, subtracting a matrix is akin to adding its negative counterpart. Here's how it looks with matrices A and B:

d = b - a

print('D=', d)

print('Shape of D is:', d.shape)

What if we attempt to add or subtract matrices of differing sizes? For instance, consider matrix E:

e = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

print('E=', e)

print('Shape of A is:', a.shape)

print('Shape of E is:', e.shape)

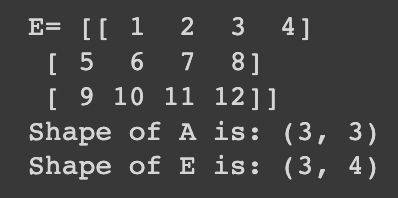
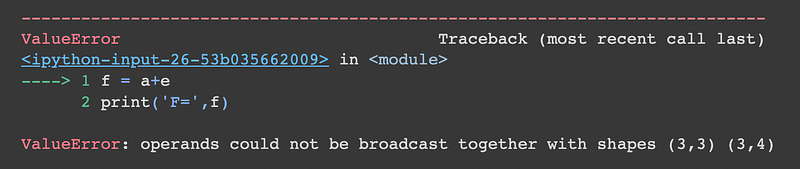
Matrix E has dimensions of 3x4, while matrix A is 3x3. As a result, attempting to add these matrices will result in an error:

f = a + e

print('F=', f)

print('Shape of F is:', f.shape)

Scalars and Matrices

When adding a scalar to a matrix, Python adds the scalar to each element within the matrix. For example:

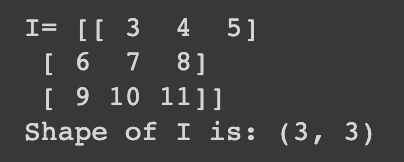
i = 2 + a

print('I=', i)

print('Shape of I is:', i.shape)

This operation can also be represented as:

j = np.array([[2, 2, 2], [2, 2, 2], [2, 2, 2]])

print('J=', j)

print('Shape of J is:', j.shape)

Multiplication

To multiply a matrix by a scalar, simply multiply each element by the scalar value. For instance, using matrix A:

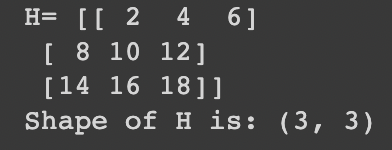
h = 2 * a

print('H=', h)

print('Shape of H is:', h.shape)

Matrix Multiplication

Matrix multiplication is more intricate and involves calculating the dot product. The dot product of two matrices is achieved by multiplying elements from the first matrix's row with those from the second matrix's column. Here's an example:

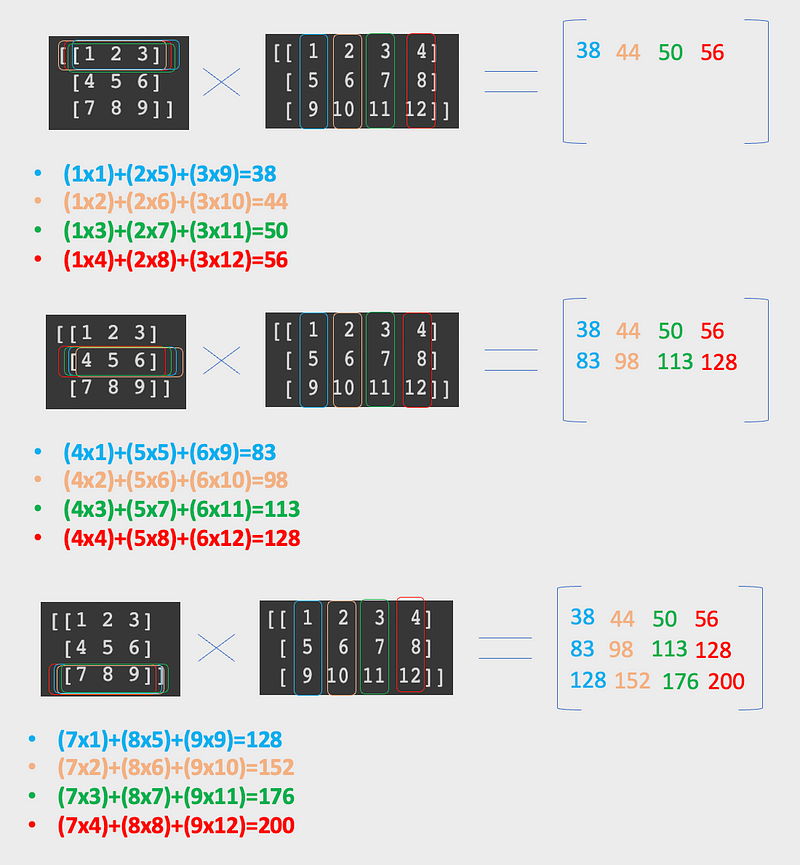
It's essential to note that for matrix multiplication to be valid, the number of columns in the first matrix must equal the number of rows in the second matrix. The resulting matrix will inherit the rows from the first and the columns from the second matrix.

Now, let's see how this works in Python with matrices A and E:

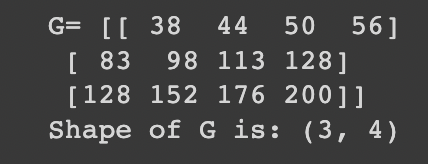
g = np.matmul(a, e)

print('G=', g)

print('Shape of G is:', g.shape)

The commutative property does not hold for matrix multiplication. Let's illustrate this with matrices A and E by reversing the multiplication order:

l = np.matmul(e, a)

print('L=', l)

print('Shape of L is:', l.shape)

To demonstrate that the commutative law is not applicable, we will compute AxB and BxA:

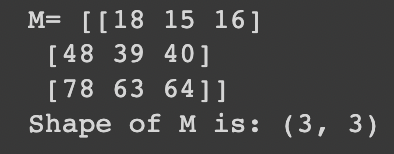
m = np.matmul(a, b)

print('M=', m)

print('Shape of M is:', m.shape)

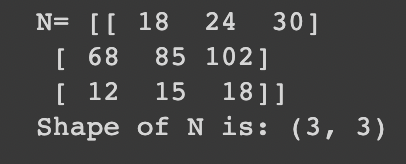
n = np.matmul(b, a)

print('N=', n)

print('Shape of N is:', n.shape)

Exceptions to the Rule: Identity Matrix

An exception exists within matrix multiplication: the identity matrix. When multiplying any matrix by an identity matrix of the same size, the commutative property holds:

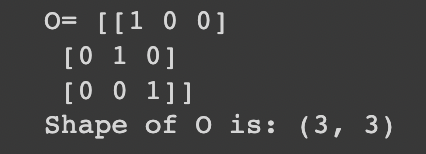
o = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

print('O=', o)

print('Shape of O is:', o.shape)

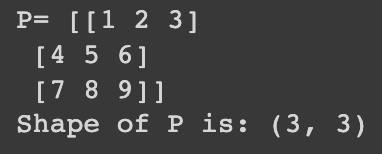
p = np.matmul(o, a)

print('P=', p)

print('Shape of P is:', p.shape)

q = np.matmul(a, o)

print('Q=', q)

print('Shape of Q is:', q.shape)

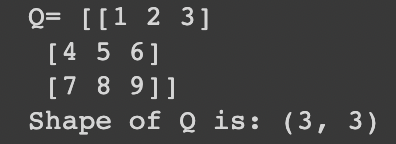
As seen, the result remains matrix A, making the identity matrix the neutral element in matrix multiplication.

References and Further Reading

• Elementary Linear Algebra, Applications Version, 9th Edition by Howard Anton and Chris Rorres.
• Maths for Computing and Information Technology by Frank Giannasi and Robert Low.