Mastering Integration by Parts: A Comprehensive Guide
Written on
Chapter 1: Introduction to Integration by Parts
The integral of e^x sin(x) stands as a classic example in the study of integration by parts. This problem can be both enlightening and rewarding. If you’re familiar with it, consider this a refreshing revisit; if not, it’s a valuable challenge worth undertaking. I suggest pausing for a moment to grab some paper and a pen before proceeding to the solution!
Solution Overview
Integration by parts is particularly useful when dealing with the product of two functions. The LIATE rule is a fundamental guideline for this technique, categorizing functions as follows:
- L = Logarithmic Functions
- I = Inverse Trigonometric Functions
- A = Algebraic Functions
- T = Trigonometric Functions
- E = Exponential Functions
When applying this rule, the goal is to select ( u ) as a function that is straightforward to differentiate, while ( dv ) should be easy to integrate. According to the LIATE rule, we should choose ( u ) from the list based on the order provided.
For this example, we’ll set ( u = sin(x) ) and consequently, ( dv = e^{x}dx ).
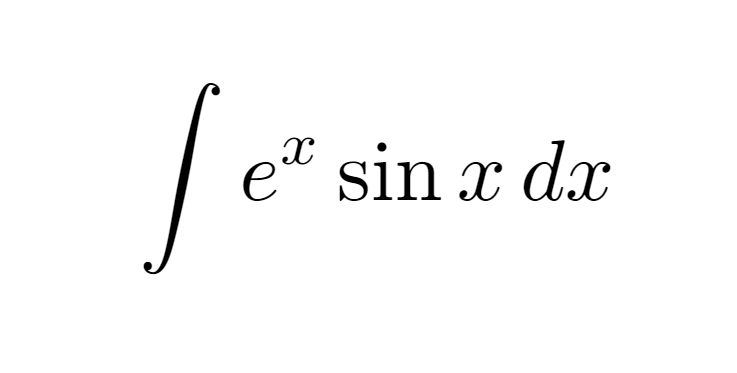
Next, we can employ the integration by parts formula, which states:
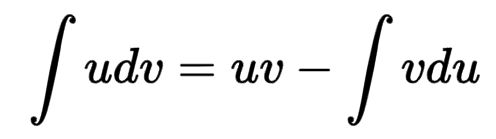
Now, substituting our selected ( u ) and ( dv ) into the right-hand side:
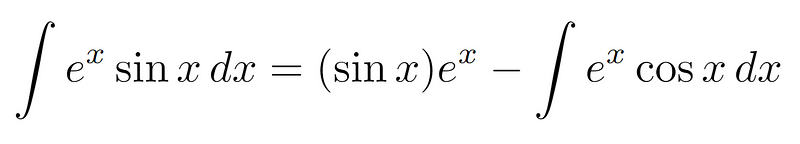
The crucial aspect of this example is that we need to apply integration by parts once again to tackle the integral of ( e^x cos(x) ). Here, we’ll again choose ( u ) as the trigonometric function, with ( dv = e^x dx ).

After determining ( dv ):

We substitute these values into the equation:
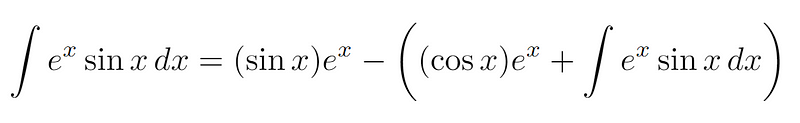
Notice that the term on the far right is equal to what we are trying to determine! This allows us to set it equal to ( I ) and solve for ( I ):
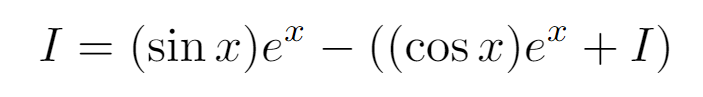
By rearranging the equation to isolate ( I ):
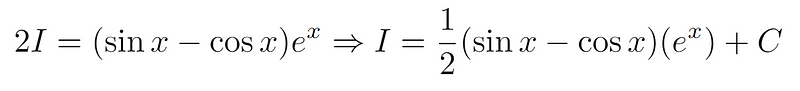
And remember to include the constant ( + C )! That’s the solution!
Bonus Challenge
As a bonus, can you evaluate the integral shown below?
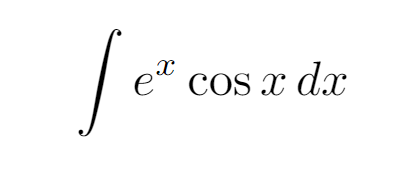
Also, what happens if we select ( u = e^x ) instead? How intriguing! I’d love to hear your thought process in the comments below!
Math Puzzles
For more engaging math puzzles, consider checking out the best math puzzles available on Medium, covering a variety of topics from Algebra to Number Theory.
The first video titled "Integration by Parts Practice Problems" offers a thorough exploration of practice problems designed to strengthen your understanding of the concept.
In the second video, "Integration by Parts Example Problems," you’ll find detailed examples that further clarify the process of integration by parts.
Thank you for your time! If you found this article useful, please consider giving it a clap and sharing it with others.
