Chapter 1: Introduction to Big O Notation

Are you able to identify an example of Big O Notation that represents a factorial algorithm? As a software engineer, it’s crucial to ensure that your algorithms are as efficient as possible. To avoid writing inefficient algorithms, you need to recognize them. This guide will help you identify Factorial and Exponential Algorithms through Big O Notation examples.

In previous discussions, we’ve examined various notations, starting from the more efficient ones like Constants and Linear, to the less efficient categories such as N Log N, Quadratic, and Cubic. If you need a refresher, consider reviewing the basics of Big O Notation.

Chapter 2: Visualizing Big O Notation

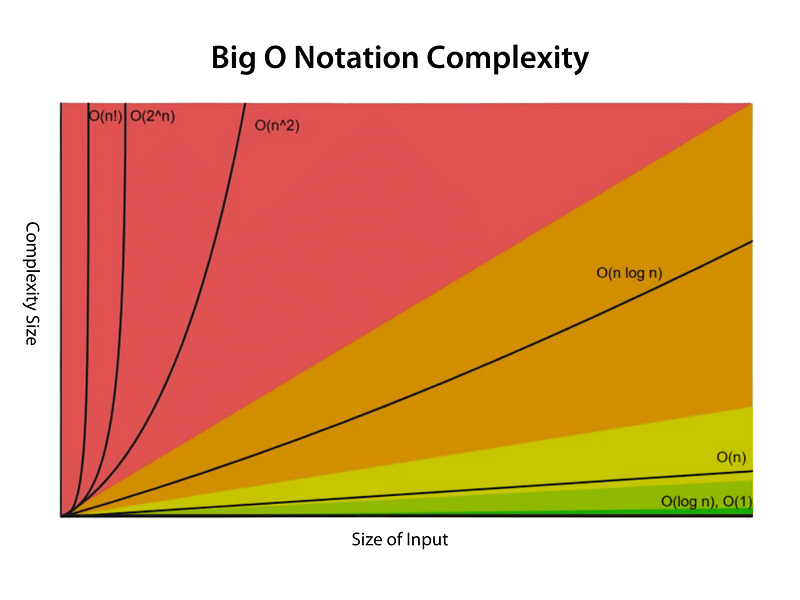
The graph above provides a clear visual representation of Big O Notation complexities, sourced from the Big O Notation Cheat Sheet—a valuable tool for understanding various notations and the algorithms associated with them.

Among the notations, two stand out for their inefficiency:

• Exponential Notation O(2^N)
• Factorial Notation O(!N)

These are the types of notations you want to avoid at all costs.

Section 2.1: Exponential Notation — O(2^N)

Exponential notation ranks as the second least efficient, as the time or space complexity doubles with each incremental increase in input. This behavior is particularly evident in recursive coding examples, where operations can quickly become unmanageable.

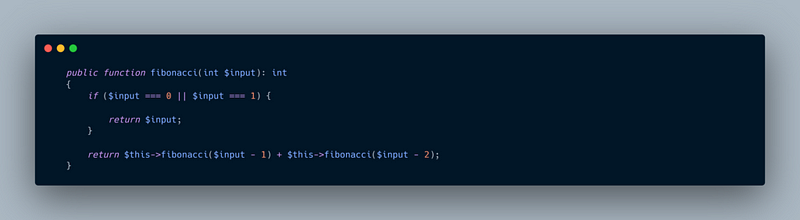
To illustrate exponential growth, consider the Fibonacci sequence. The code may appear straightforward, but its inefficiency is significant:

This video explains the Big O of N factorial in greater detail, helping you grasp the implications of exponential growth.

In this PHP example, we set a base case:

if ($input === 0 || $input === 1) {

return $input;

}

For inputs greater than 1, the function calls itself twice, leading to exponential complexity.

The flowchart demonstrates how the processing time doubles with each new level of input. While this may work for smaller inputs, it can become problematic in a production environment where efficiency is crucial.

Section 2.2: Factorial Notation — O(!N)

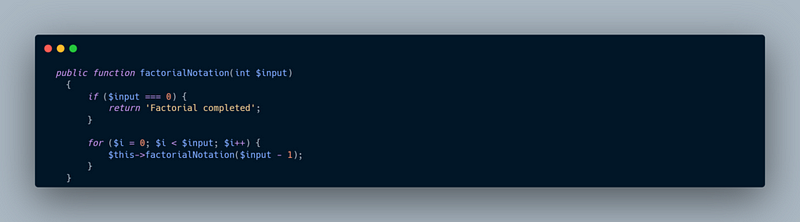
Factorial notation is the least efficient of the algorithms. This is typically observed when the complexity of an algorithm grows as the product of the input size and all smaller integers.

For instance, with an input of 5, the calculation is:

5 x 4 x 3 x 2 x 1 = 120

With an input of 10, it becomes:

10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 3,628,800

The inefficiency becomes glaring as input sizes grow.

In PHP, a simple implementation of factorial notation might look like this:

if ($input === 0) {

return 1;

} else {

return $input * factorial($input - 1);

}

The video above elaborates on the types of time and space complexities, including factorial growth, providing further insights into these concepts.

With an input of 3, the factorial results in:

3 x 2 x 1 = 6

This process illustrates how an algorithm is classified as factorial, based on the final output being the product of the input and all preceding integers.

Chapter 3: Key Takeaways for Big O Notation

When working with Big O Notation, keep these principles in mind:

1. Eliminate Constants: When analyzing algorithms, ignore constants to focus on the most significant factors affecting performance.
2. Prioritize Inefficiency: Concentrate on the least efficient notation, as this will dictate overall performance.

Understanding Big O Notation enhances your skills as a software engineer. By recognizing different notations, you can evaluate the performance of your code and its potential impact on your systems.

When designing features, consider future scalability. A feature that retrieves data for a single client may not need to be efficient today, but if requirements change, that same code might need to handle reports for all clients. Designing for extensibility means prioritizing efficient algorithms, which will not only facilitate smoother operations but also impress during technical interviews when the topic of Big O Notation arises.