Chapter 1: Introduction to Quantum Mechanics and Gradient Descent

In this article, we will delve into a numerical approach that has broad applications in quantum mechanics and quantum chemistry, despite its infrequent appearance in textbooks. Our objective is to address the stationary Schrödinger equation in its most comprehensive form:

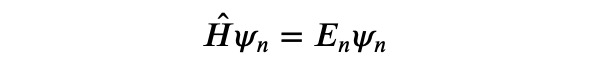
Here, ? represents the Hamiltonian operator, while ?_? signifies an eigenvector (wave function) of the Hamiltonian, and ?_? denotes the corresponding energy eigenvalue. Our aim is to compute the various eigenvectors along with their associated energies, particularly focusing on the ground state, defined as the eigenvector with the least energy.

The technique we will explore is a variant of gradient descent, cleverly disguised. Let’s consider the result of applying ? to an arbitrary initial wave function ?_init. We can express ? in terms of the eigenvectors, which remain unknown for now:

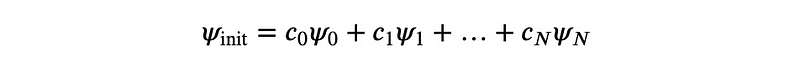
In this context, ?_0 will denote the eigenvector with the minimum energy, while ?_? represents the one with the maximum energy. Consequently, we observe that:

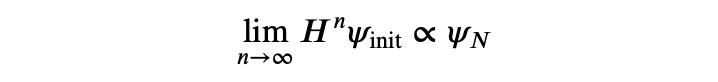
The term with the highest eigenvalue increasingly dominates the other terms, leading to the conclusion that only this term prevails in the limit, thus orienting the resulting vector entirely towards ?_?.

This raises an intriguing question: how can we obtain the eigenvector with the lowest eigenvalue? The solution is straightforward. By applying a linear mapping to ?, we can derive another operator possessing the same eigenvectors, but with reversed eigenvalues. A simple choice for this operator is:

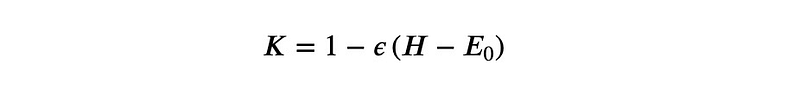
When we apply this operator to an eigenvalue of ?, we get:

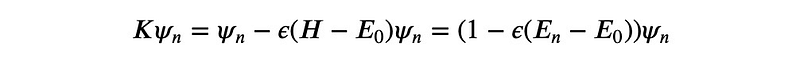
This means that the eigenvectors of ? also serve as eigenvectors of ?, albeit with different eigenvalues. For the H-eigenvector ?_0, associated with the lowest H-eigenvalue ?_0, we find:

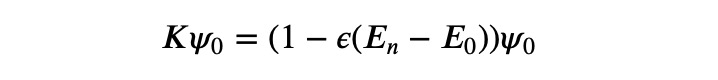
Thus, the corresponding K-eigenvalue remains under 1.

Conversely, for the H-eigenvector ?_? linked to the highest H-eigenvalue ?_?, we observe:

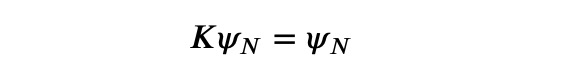
This indicates that the spectrum is effectively reversed. Now, we can utilize this principle to iterate towards the K-eigenvector with the maximum K-eigenvalue, which corresponds to the H-eigenvector with the minimum H-eigenvalue, or the ground state.

The detailed iteration process is as follows, where the upper index in brackets denotes the iteration count:

1. Begin with a normalized wave function:

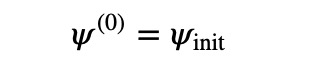
2. Iterate using the formula:

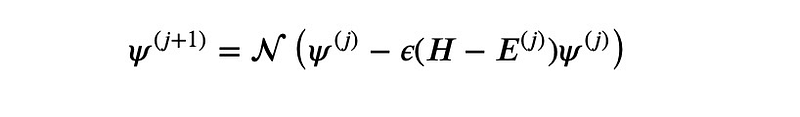
Here,

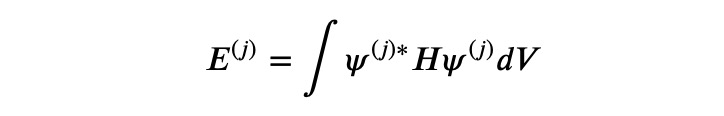
and N represents the normalization operation:

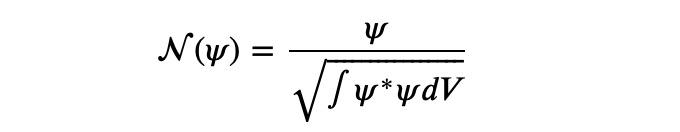
We normalize at each step to maintain the range of valid floating-point numbers.

Choosing the appropriate step size, denoted as ?, is crucial. Typically, it should be:

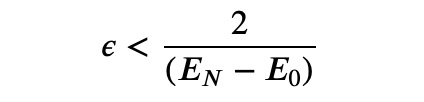
However, since the energies are unknown in advance, this information is not particularly useful. While there are advanced techniques available for determining an optimal step size, simple experimentation will suffice for our purposes.

Now, why do I refer to this as gradient descent in disguise? The reason is that ?? is directly linked to the functional derivative of the energy concerning the wave function:

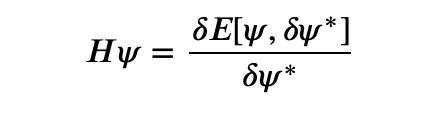
where ? signifies the functional derivative. Thus, this methodology effectively embodies a gradient descent approach.

Let’s encapsulate this process in a general routine for our gradient descent:

import numpy as np

def gradient_descent(H, n_steps, eps, psi_init, integral):

def normalize(psi):

return psi / np.sqrt(integral(psi**2))

psi = normalize(psi_init)

for j in range(n_steps):

E = integral(psi * H(psi))

psi = normalize(psi - eps * (H(psi) - E * psi))

E = integral(psi * H(psi))

return psi, E

This function is designed to be versatile, applicable to a wide range of problems. Let's apply it to the 1D harmonic oscillator as our first case. We need to define the Hamiltonian and the integral operator:

from findiff import FinDiff

x = np.linspace(-5, 5, 100)

dx = x[1] - x[0]

laplace = FinDiff(0, dx, 2)

V = 0.5 * x**2

def H(psi):

return -0.5 * laplace(psi) + V * psi

def integral(f):

return np.trapz(f) * dx

Now, we can compute the ground state of the harmonic oscillator:

psi = np.exp(-np.abs(x))

psi, E = gradient_descent(H, 100, 0.01, psi, integral)

E # Output: 0.4997480777288626

The exact value should be 0.5.

Next, let’s consider the hydrogen atom:

x = y = z = np.linspace(-10, 10, 80)

dx = dy = dz = x[1] - x[0]

laplace = FinDiff(0, dx, 2) + FinDiff(1, dy, 2) + FinDiff(2, dz, 2)

X, Y, Z = np.meshgrid(x, y, z, indexing='ij')

R = np.sqrt(X**2 + Y**2 + Z**2)

V = -2 / R

def H(psi):

return -laplace(psi) + V * psi

def integral(f):

return np.trapz(np.trapz(np.trapz(f))) * dx * dy * dz

psi = np.exp(-R**2)

psi, E = gradient_descent(H, 600, 0.01, psi, integral)

E # Output: -0.9848171001223128

The expected value here is -1, indicating that our result is somewhat crude due to the singularity present at the origin. However, this topic warrants further exploration.

There's a wealth of additional concepts we could discuss, such as constraints for calculating excited states, which will be covered in a future post. Stay tuned, and thank you for reading!

Chapter 2: Video Resources

To enhance your understanding of the Schrödinger equation and gradient descent, here are two insightful video resources:

Learn how to solve the Schrödinger equation quickly using Python and GPU acceleration.

Explore two techniques for solving the time-dependent Schrödinger equation in Python.