Chapter 1: Introduction to the Action Principle

The fascinating world of physics often reveals that nature prefers to take the easiest route. At the heart of modern physics lies the action principle, a concept that influences every branch of the discipline. Instead of drowning in intricate mathematical details, we will journey from the behavior of light in water to the realms of quantum mechanics. By the end, you should gain a deeper appreciation for the elegance of physics.

Chapter 1.1: Light's Journey and Fermat's Principle

Let's begin by examining a ray of light transitioning from air into water. Picture a light ray originating from point A in the air and heading to point B in the water. Intuitively, one might think it would take a straight path to minimize distance. However, that is not the case; the light ray bends at the interface between air and water.

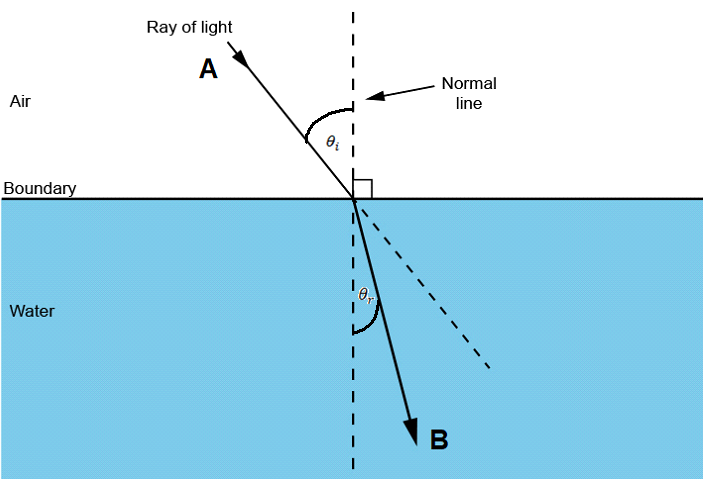
But why does this occur? In 1662, Pierre de Fermat provided the answer, asserting that light always travels along a path that minimizes its travel time. This principle informs us that light’s journey between two points adheres to the least time principle. By considering that the speed of light changes in different mediums, we can derive Snell's law of refraction, which helps us calculate the angles at which light enters and exits various materials.

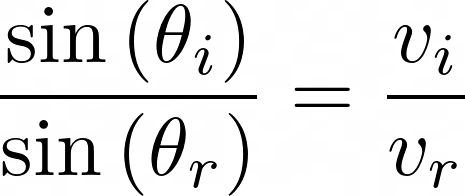
Chapter 1.2: The Concept of Action

Previously, we saw how light chooses the path that reduces travel time. In 1788, Joseph-Louis Lagrange extended this idea, proposing that any particle in motion also minimizes its action. The action principle posits that a moving particle will always opt for the trajectory that minimizes its action.

But what do we mean by "action"? In a mechanical context, such as a ball thrown through the air, the action ( S ) has a specific mathematical definition.

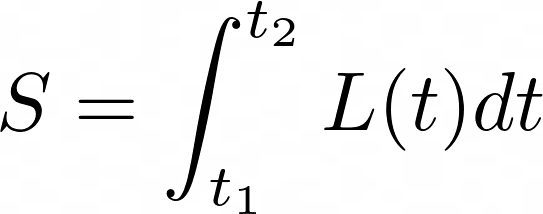
While this definition may appear complex, it can be understood conceptually through high school calculus. Here, ( L ) represents the Lagrangian of the system, defined as the difference between kinetic energy ( T ) and potential energy ( V ).

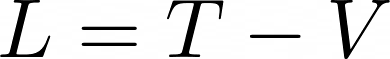
We denote it as ( L(t) ) to indicate its dependence on time, which varies as the object moves. The action is derived from the integral of the Lagrangian over time, representing the area under the curve ( L(t) ) between time ( t_1 ) and ( t_2 ). Although the Lagrangian lacks physical significance, it serves a critical mathematical purpose.

How do we determine the path that minimizes ( S )? The solution lies in the Euler-Lagrange equation, which helps identify this optimal trajectory.

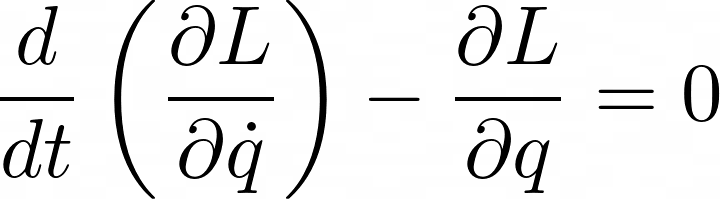
While the mathematical intricacies are not our main concern, remember that inserting the system's Lagrangian into the Euler-Lagrange equation yields its equations of motion, defining the most efficient path. Returning to our earlier example of a thrown ball, applying its Lagrangian into the equation results in a parabolic trajectory, assuming negligible air resistance.

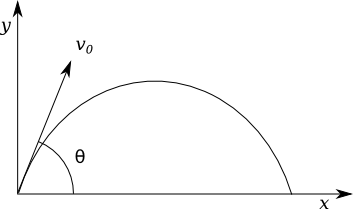
Chapter 2: Quantum Mechanics and Infinite Paths

What happens on a smaller scale, such as with an electron? In these instances, we turn to quantum mechanics. Richard Feynman, in 1948, utilized the action principle to develop quantum mechanics through the path integral formulation.

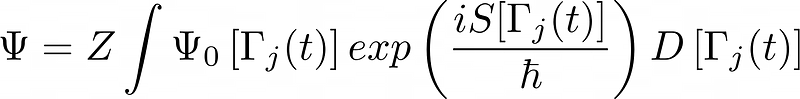
Earlier, we learned that a particle follows a distinct path that minimizes its action between two points. However, in quantum mechanics, this certainty disappears. We cannot pinpoint the exact path a particle takes from A to B; instead, we consider the probability of its journey.

Even the most renowned physicists, including Einstein, struggled with the peculiarities of quantum mechanics. He famously remarked, “God does not play dice with the universe.”

Now that we've touched upon these quantum anomalies, it's time to explore the path integral. To address our earlier inquiry, we must evaluate the path integral of the quantum system, taking into account the infinite potential paths between points A and B.

Not all potential paths possess an equal probability of occurring. Each is assigned a probability amplitude, and the overall likelihood of the particle traveling from A to B is determined by summing the amplitudes of all conceivable paths, however improbable they may be.

The action principle becomes relevant here: paths that are more plausible have smaller actions ( S ) and correspondingly larger probability amplitudes, while less likely paths exhibit larger actions and smaller amplitudes. Thus, we can conclude that—

The most probable paths, characterized by the smallest actions ( S ), contribute significantly to the likelihood of the particle's journey from A to B.

This encapsulates the essence of Feynman's path integral. There remains much to explore, but I hope this discussion has illustrated that physics transcends mere calculations; it is about unraveling the mysteries of the universe.

Did you enjoy this article? Consider giving it some claps to support my work, or feel free to tip via the button below. For more content like this, follow me; I aim to publish monthly. References and further reading can be found here.

This video delves into the principle of least action and its significance in physics, illustrating its foundational role in understanding the universe.

An exploration of whether action is the most fundamental property in physics, examining its implications in both classical and quantum realms.