Exploring Area Proofs in Quadrilaterals: A Mathematical Journey
Written on
Chapter 1: Introduction to Area Proving
In this discussion, we delve into a problem from the British Mathematical Olympiad (Round 1, 2007). We are given a convex quadrilateral ABCD, where points M and N are positioned on side AB so that AM = MN = NB. Similarly, points P and Q divide side CD such that CP = PQ = QD. The task is to demonstrate that the Area of AMCP equals the Area of MNPQ, which together comprise one-third of the Area of ABCD.
To clarify any potential misunderstandings, I've included diagrams that illustrate the configuration of the quadrilaterals involved.
Here’s a diagram representing the quadrilaterals and their relationships.
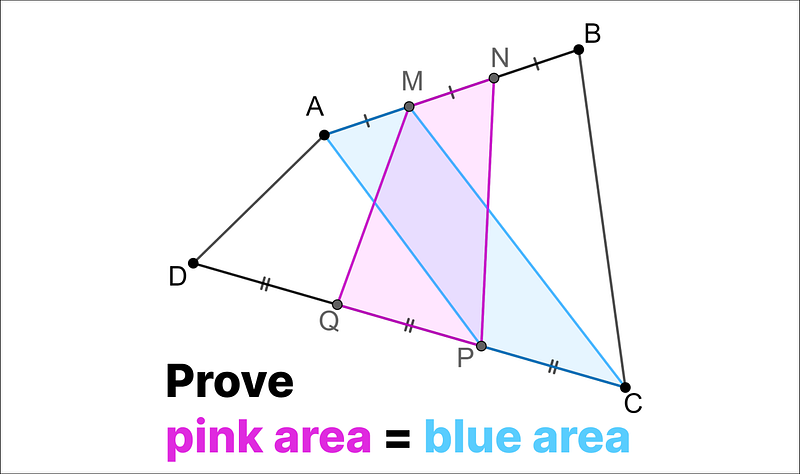
There are various methods to show that the areas of the pink and blue quadrilaterals are equal. I believe the approach I'll outline is particularly elegant.
Section 1.1: Decomposing Quadrilateral AMCP
We start our analysis with the blue quadrilateral AMCP, which we can divide into two triangles for easier examination.
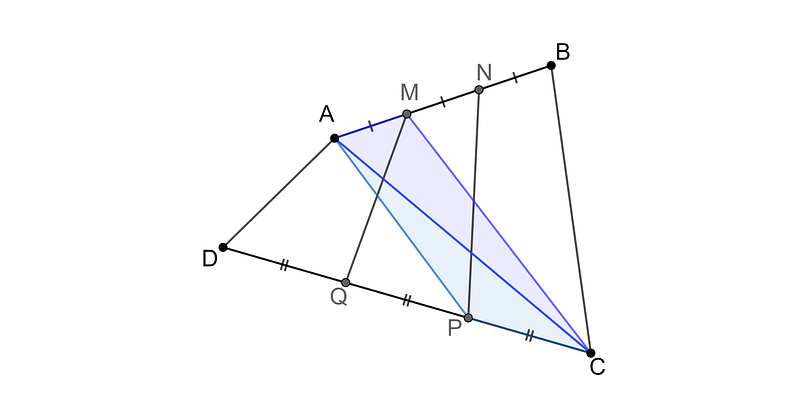
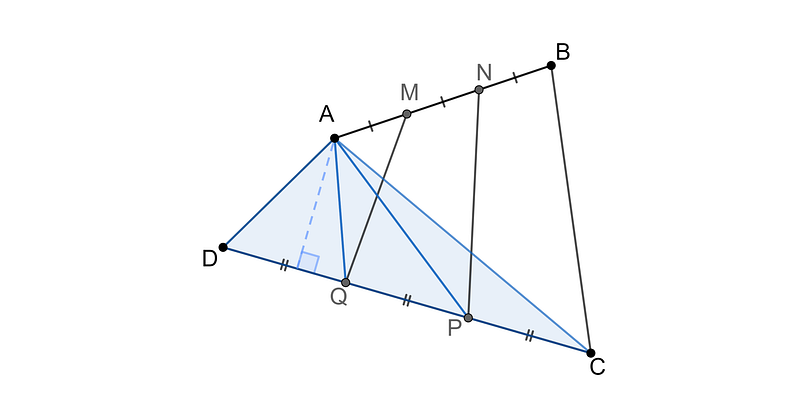
Next, we direct our attention to triangle ACP. By considering segment PC as its base and drawing a perpendicular from point A to line DC, we can determine that triangle ACP shares the same area with triangles APQ and AQD.
This observation is advantageous, as we can apply the same reasoning to triangles CBN, CNM, and CMA, which form the remainder of the quadrilateral.
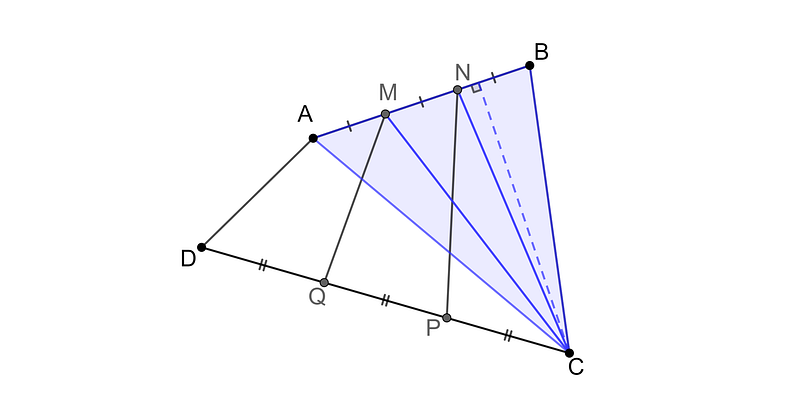
We've established that quadrilateral ABCD can be expressed as
3 × Area(ACP) + 3 × Area(CMA).
Consequently, we can conclude that quadrilateral AMCP occupies one-third of the total area of ABCD.
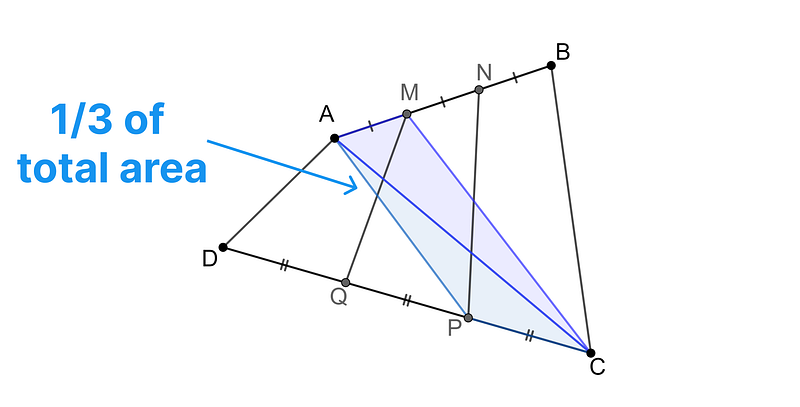
Now, we turn our focus to proving that quadrilateral MNPQ has an identical area. By excluding triangles AQD on the left and CBN on the right—together accounting for one-third of the area—we find that quadrilateral ANCQ retains two-thirds of the total area.
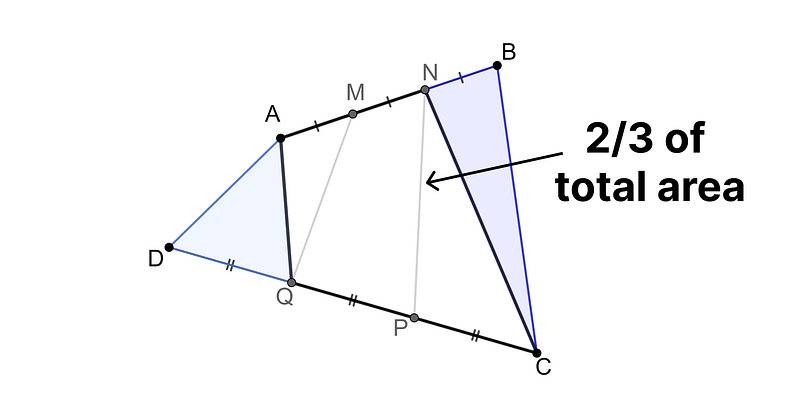
We can further dissect this central quadrilateral into two pairs of triangles, each sharing equal areas (utilizing the same logic as before, these triangles have equal bases and heights).
The equalities are as follows:
Area(QAM) = Area(QMN)
Area(NCP) = Area(NPQ)
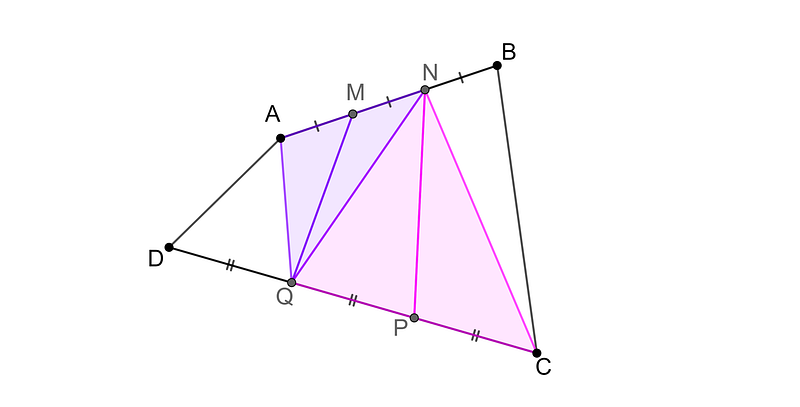
After eliminating the two outer triangles, we are left with:
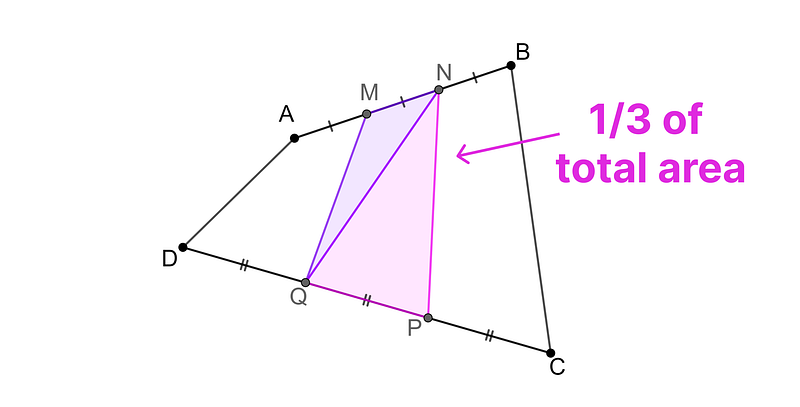
Quadrilateral MNPQ also occupies one-third of the total area of quadrilateral ABCD. Isn’t that fascinating?
Here’s a concise video summarizing the solution, accompanied by uplifting music from Adam Levine:
Chapter 2: Video Resources for Deeper Understanding
The first video titled "If the areas of two similar triangles are equal, prove that they are congruent" provides a fundamental understanding of congruence in geometry.
The second video titled "Ratios of Areas" explores the relationships between areas of different geometric shapes, enhancing our comprehension of spatial reasoning.